It's hard to believe I've been posting for over a year and a half and I still haven't gotten around to talking about the case of the crystal radio, which was my personal epiphany on the road to quantum mechanics. I started toying around with the question when I was in fourth-year engineering: specifically, how much power could you absorb with a well-designed crystal radio set?
There was a time when everyone knew what a crystal radio was. There was no electricity out on the farms, and batteries were expensive. Ingenious people figured out that they could pick up radio stations with little more than an antenna, an earphone, a tuning coil and something called a "crystal".
The crystal is actually the least important part of the discussion which follows; all it does is rectify the radio-frequency power so it is audible in the earphone. From the perspective of energy flow, the power has already been absorbed before it is rectified. So we're going to ignore the crystal from here on in. The question is: given a fixed amount of power density from the distant radio transmitter, how much can you absorb with your small receiver station?
It seems obvious that the key to absorbing power lies in the design of the antenna; obviously, a bigger antenna will absorb more power than a smaller one. The problem is that the actual mechanism of power absorption by an antenna is somewhat obscure. People talk about an induced voltage, and in engineering class we did a lot of calculations on the voltage for different antenna configurations. But we never converted this into power. I knew there was something called the "radiation resistance" of an antenna, and that for maximum power transfer you wanted to match the radiation resistance to the resistance of the load (that would be the earphone); but none of this made much physical sense. How would you calculate this so-called "radiation resistance", and what was its physical meaning?
This went on for several years without much progress. Then I got in a discussion with some professors and one of them said that there was a simple formula for radiation resistance, and it went as the square of the antenna length. I had already given some thought over the years to the implications of various length dependencies, and had quickly ruled out a quadratic relationship because in combination with the well-known V-squared-over-R formula, it would imply that the theoretical absorbed power was independent of antenna length. I tried to make this point but the professor simply wandered off.
Still, something was fishy. I don't know how it came to me but I started drawing picturtes of radio waves: straight plane waves arriving from a distant stationon the left, and circular outgoing waves emanating from the receiving antenna as a result of the currents induced in it. Something like this:
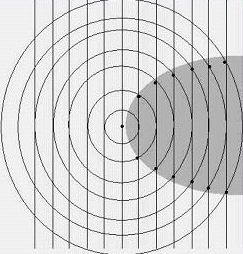
Notice that within the shaded region behind the antenna, the phase difference between the incoming and outgoing waves is everywhere less than 180 degrees; so within this zone, and only within this zone, there is the prospect of destructive interference. Why do I say the "prospect"? Because the nature of the interference will depend on the exact relative phase of the two wave patterns.
The amazing thing is we can do a rough calculation on the energy balance from this simple picture. Over most of the spherical surface of the outgoing wave, power is simply being re-radiated, or in other words, wasted. It is only in the shadow region that we can absorb the power that will ultimatley be delivered to the earphone. And here is the key: in the shadow region, the power removed from the incoming wave is in linear proportion to the induced current. In the remainder of the spherical area, the power re-radiated is proportional to the
square of the current.
Now, whenever you have two quantities, and one is linear and the other is quadratic, the linear one dominates at first; but then the quadratic grows faster, so it catches and overtakes the linear term. What this means for the antenna is that as you draw current and deliver it to the load, at first you have power available because the power you remove from the shadow zone is greater than the power you waste re-radiating into the rest of space. But as you try to draw more power from the antenna, the wasted power grows much faster than the useful power. The maximum current in the antenna flows when the load is short circuited; in that case, the power removed from the shadow zone is exactly equal to the power re-radiated to the rest of space. The maximum absorbed power is obtained at exactly one-half of this short-circuit current.
How do we contrive to get just the right amount of current to flow? This is called "matching the load impedance". And returning to the question we raised earlier: how do we arrange so that the relative phases of the two wave systems are just right so that there is maximum destructive interference in the shadow zone? This is called "tuning" the antenna, and it is the reason you have a tuning coil.
What does this have to do with quantum mechanics? The amazing thing in this calculation is that we have determined the amount of power we can absorb from an external wave, and nowhere in the calculation did we need to worry about the size of the receiving antenna! It doesn't matter how small you make the antenna: you can still absorb just as much power. Of course, there are practical limitiations; because of the electrical resistance of copper, you cannot easily demonstrate this effect with ordinary AM-radio receivers. However, the result is true in principle, and incredibly enough, nature provides us with abundant examples of perfectly ideal, lossless antenna systems. They are called "atoms" and they are everywhere.
What the crystal radio teaches us is that the absortive capacity of an atom at its resonant frequency is independent of the size of the atom. At least, this is what it should teach us if we are paying attention. But if we look at any high-school physics textbook, it tells us that classical physics cannot explain the photo-electric effect because the cross-sectional area of an atom is much too small to absorb the amount of energy needed to eject an electron from an atom. Hence the photon!
What the books don't say is that according to the same argument, a crystal radio shouldn't work. Because the antenna is made of a thin wire, and if you calculate the amount of energy actually falling on that wire, it is much to small to drive even the tiniest speaker. It's the same argument.
Does the crystal radio work? I will give the final word to my father. He grew up in the depression, and when I first got interested in this topic I asked him if he had ever heard of a crystal radio. "Oh, sure," he said. Did he get one to work? "I never saw one work. The Ukranian kids could make them work." (The North End of Winnipeg was characterized in those days by its ethnic population composed largely of Ukranians and Jews.)
It's funny that the Jews come in handy when you need to do something super technical like inventing the atom bomb or finding the cure for polio, but we don't seem to have the most practical hands-on skills in everything. I guess it goes to show that it takes all kinds.

4 comments:
Hi
I got this from:
Can the photoelectric effect be explained without photons?
http://physics.stackexchange.com
------------------------------
I explain this in my blogpost on the crystal radio. (And I don't think anyone wants to argue that you need photons to explain the crystal radio.)
--------------------------------
When I read your blogpost it seems that you 'are' saying a crystal radio can be explained by classical electromagnetic waves
But: (And I don't think anyone wants to argue that you need photons to explain the crystal radio.)
Seems to be saying a crystal radio can "only" be explained by photons
What am I reading wrong here ??
Thanks
Peter
You may be overthinking that last phrase. Remember, "argue" has two meanings: to dispute, or to assert. If you read the sentence with the latter meaning, it makes sense in the obvious way.
Maybe you might like engineering reasoning better than physics. I saw this related to your subject.
http://www.the-phoney-photon.com/#Antenna_theory
Any how my comment on your wave analysis of the antena is this. A circuit that receives energy/power from an antenna absorbs part of it into the circuit. So, the process is not total reflection but partial or full absorption. Conservation of energy principle.
Notice where the strait line is midway between the circles there is constructive interference giving double amplitude with your reflection theory?
Post a Comment